Edit on GitHub

Notes

Structures

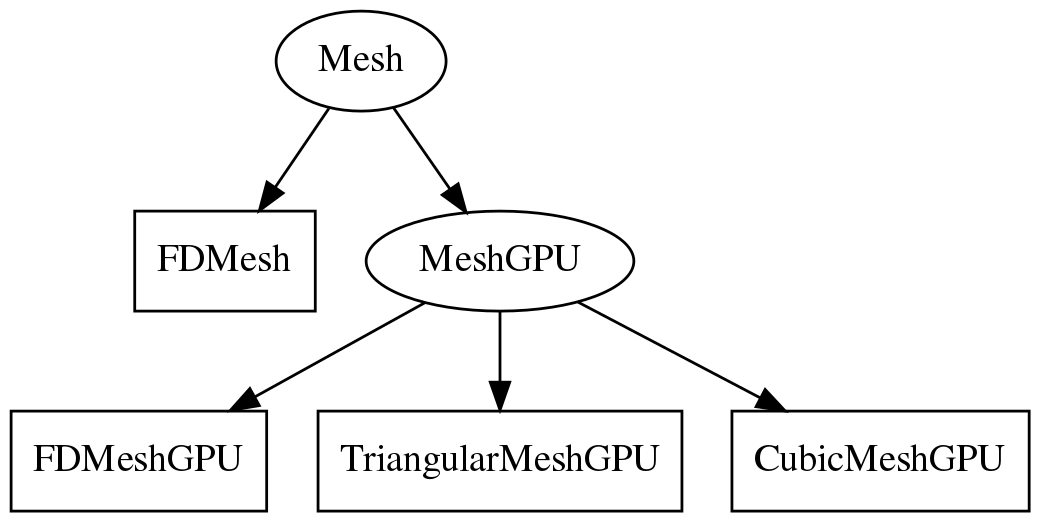
Mesh

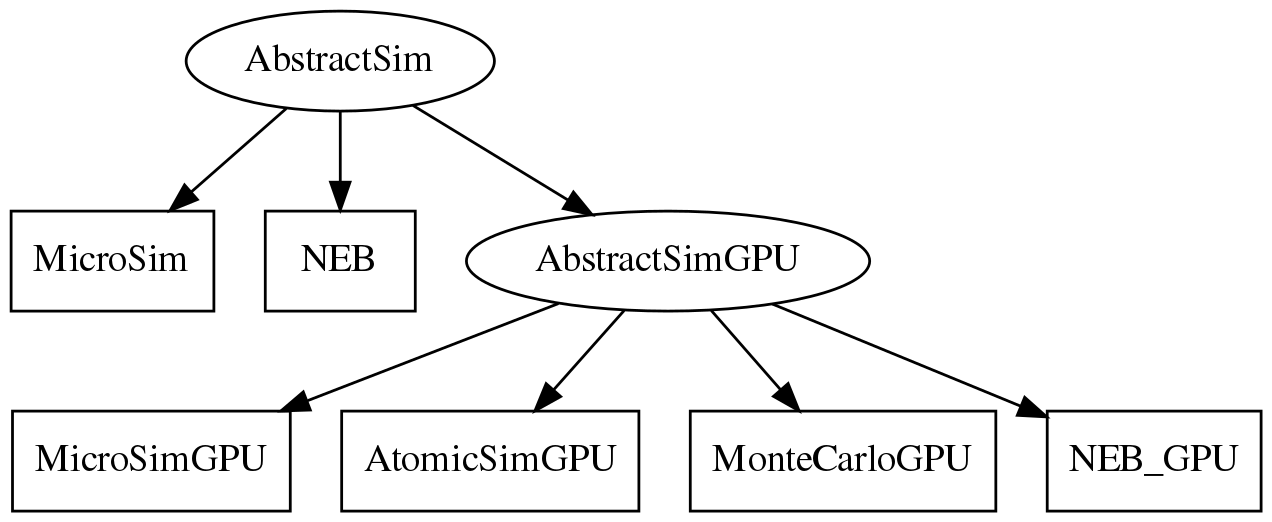
Sim

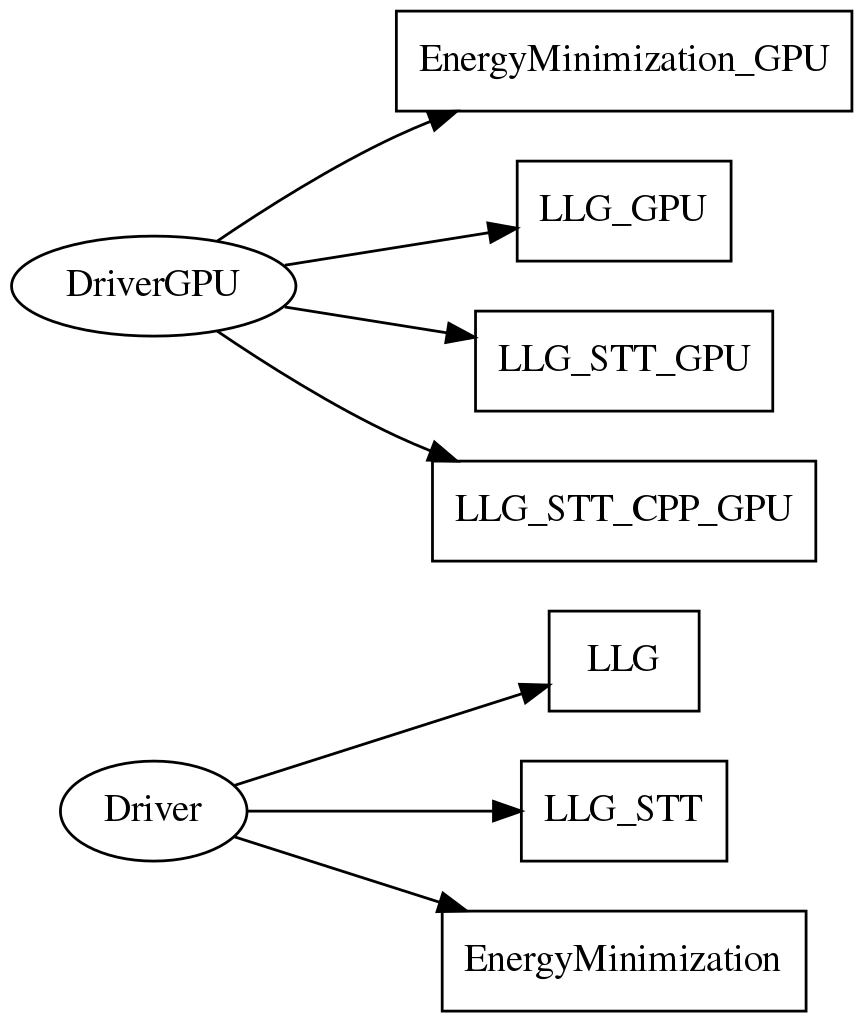
Driver

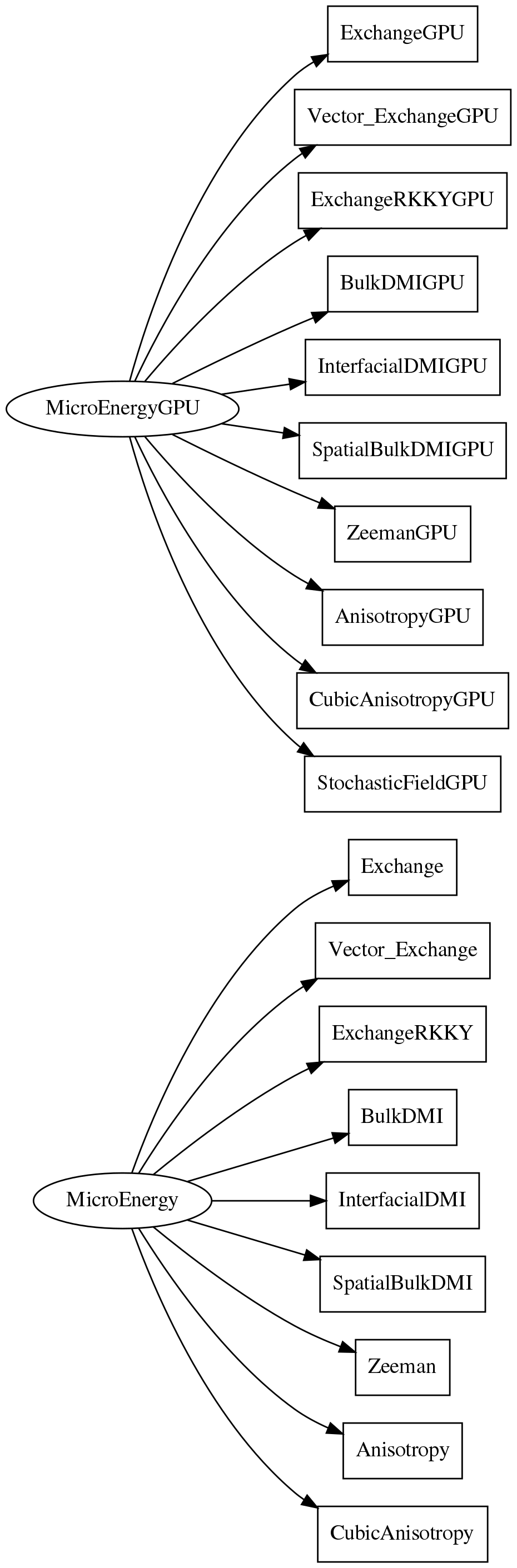
Energy

Reducing the startup time

Julia is a dynamically-typed language, so the input script will be compiled when we start a simulation. However, the typical startup time in our case ranges from 1s to 30s depends on the complexity of the problem. It is painful especially if we run the simulation using GPU. Luckily, we can compile our package using PackageCompiler.jl:

using PackageCompiler
compile_incremental(:JuMag)

After finishing the compilation, a dyn.so file will be generated. If we start julia using julia -J /path/to/dyn.so the stratup time will be ignorable.

Note: If you got an error similar to that shown at https://github.com/JuliaLang/PackageCompiler.jl/issues/184, using dev PackageCompiler may solve the issue.

If other errors appear, it is better to figure out which package is failed

compile_incremental(:FFTW, :CUDAdrv, :CUDAnative, :CuArrays, force=false)

and remove that package from deps in Project.toml. For example, if CuArrays fails, comment the line

#CuArrays = "3a865a2d-5b23-5a0f-bc46-62713ec82fae"

may solve the problem.

LLG equation with Zhang-Li extension

\[\frac{\partial \vec{m}}{\partial t} = - \gamma \vec{m} \times \vec{H} + \alpha \vec{m} \times \frac{\partial \vec{m}}{\partial t} + u_0 (\vec{j}_s \cdot \nabla) \vec{m} - \beta u_0 [\vec{m}\times (\vec{j}_s \cdot \nabla)\vec{m}]\]

where

\[u_0=\frac{p g \mu_B}{2 |e| M_s}=\frac{p g \mu_B a^3}{2 |e| \mu_s}\]

and $\mu_B=|e|\hbar/(2m)$ is the Bohr magneton. In LL form

\[(1+\alpha^2)\frac{\partial \vec{m}}{\partial t} = - \gamma \vec{m} \times \vec{H} - \alpha \gamma \vec{m} \times (\vec{m} \times \vec{H}) + (1+\alpha\beta) u_0 \vec{\tau} - (\beta-\alpha) u_0 (\vec{m}\times \vec{\tau})\]

where $\vec{\tau}=(\vec{j}_s \cdot \nabla)\vec{m}$

Note that

\[u_0 (\vec{j}_s \cdot \nabla) \vec{m}= - u_0 \vec{m}\times[\vec{m}\times (\vec{j}_s \cdot \nabla)\vec{m}]\]

so this torque is damping-like torque and the last torque is field-like torque. Therefore, we rewrite the LLG equation in the form

\[\frac{\partial \vec{m}}{\partial t} = F(\vec{m}) \times \vec{m}\]

where

\[F(\vec{m}) = \frac{1}{(1+\alpha^2)} [\gamma \vec{H} + u_0 (\beta-\alpha)\vec{\tau}]+ \frac{1}{(1+\alpha^2)}\vec{m} \times [\alpha \gamma \vec{H} + u_0 (1+\alpha\beta) \vec{\tau}]\]

Cayley transformation

The LLG equation can be cast into

\[\frac{\partial \vec{m}}{\partial t} = \hat{F}(\vec{m}) \cdot \vec{m}\]

where the operator \hat{} is defined as

\[\hat{x} = \left( \begin{matrix} 0 & -x_3 & x_2 \\ x_3 & 0 & -x_1 \\ -x_2 & x_1 & 0 \end{matrix} \right)\]

Using the Cayley transfromation, the LLG equation can be written as

\[\frac{\partial \Omega}{\partial t} = F - \frac{1}{2} [\Omega, F] - \frac{1}{4} \Omega F \Omega\]

where

\[\Omega = \hat{\omega}\]

So one has

\[\frac{\partial \vec{\omega}}{\partial t} = \vec{F} - \frac{1}{2} (\omega \times \vec{F}) + \frac{1}{4} (\omega \cdot \vec{F}) \vec{\omega}\]